6.2. NZS3101:2006#

class NZS3101[source]

Design code class for the New Zealand concrete design standard NZS3101:2006. Also implements the requirements of the NZSEE C5 assessment guidelines for probable strength design.

Note

Note that this design code currently only supports Concrete and NZS3101.SteelBarNZ material objects. Meshed Steel material objects are not supported as this falls under the composite structures design code.

Inits the NZS3101 class.

Using the NZS3101:2006 design code starts by creating an NZS3101 object:

from concreteproperties.design_codes.nzs3101 import NZS3101

design_code = NZS3101()

After a ConcreteSection object has been created it must be assigned to the design code:

design_code.assign_concrete_section(concrete_section=concrete_section)

NZS3101.assign_concrete_section(concrete_section, section_type='column')[source]

Assigns a concrete section and the section type for the concrete section to the design code.

Parameters

concrete_section (ConcreteSection) – Concrete section object to analyse
section_type (str, default: 'column') –
The type of member being analysed:-
- column - Analyses assigned concrete section object as a column (or beam) member in accordance with NZS3101:2006 Chapter 9 or 10 as appropriate
- wall - Analyses assigned concrete section object as a doubly reinforced wall member in accordance with NZS3101:2006 Chapter 11
- wall_sr_s - Analyses assigned concrete section object as a singly reinforced wall member in accordance with NZS3101:2006 Chapter 11 for design actions causing bending about the strong axis
- wall_sr_m- Analyses assigned concrete section object as a singly reinforced wall member in accordance with NZS3101:2006 Chapter 11 for design actions causing bending about the minor axis

Raises

ValueError – If the concrete section contains meshed reinforcement
ValueError – If section type for the analysis of the concrete section is not valid

Return type

None

Note

To maintain unit consistency, the cross-section dimensions should be entered in [mm].

6.2.1. Creating Material Properties#

The NZS3101 class can be used to easily create material objects whose attributes comply with the standard.

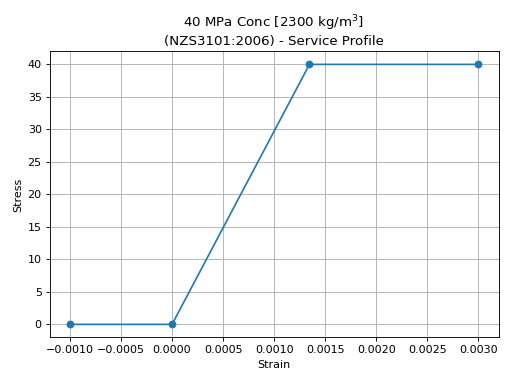
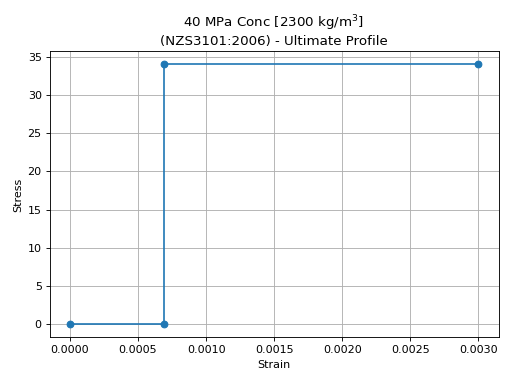
NZS3101.create_concrete_material(compressive_strength, ultimate_strain=0.003, density=2300, colour='lightgrey')[source]

Returns a concrete material object to NZS3101:2006.

Material assumptions

Density: Defaults to 2300 kg/m³ unless supplied as user input
Elastic modulus: Calculated from NZS3101:2006 Eq. 5-1
Serviceability stress-strain profile: Linear with no tension
Ultimate stress-strain profile: Rectangular stress block, parameters from NZS3101:2006 CL 7.4.2.7, maximum compressive strain of 0.003
Lower characteristic tensile strength of concrete: Calculated from NZS3101:2006 Eq. 5-2

Parameters

compressive_strength (float) – 28 day compressive design strength (MPa)
ultimate_strain (float, default: 0.003) – Maximum concrete compressive strain at crushing of the concrete for design
density (float, default: 2300) – Saturated surface dry density of concrete material
colour (str, default: 'lightgrey') – Colour of the concrete for rendering, defaults to ‘lightgrey’

Returns

Concrete – Concrete material object

from concreteproperties.design_codes.nzs3101 import NZS3101

design_code = NZS3101()
concrete = design_code.create_concrete_material(compressive_strength=40)

concrete.stress_strain_profile.plot_stress_strain(
  title=f"{concrete.name} - Service Profile"
)
concrete.ultimate_stress_strain_profile.plot_stress_strain(
  title=f"{concrete.name} - Ultimate Profile"
)

(Source code)

(png, hires.png, pdf)#

(png, hires.png, pdf)#

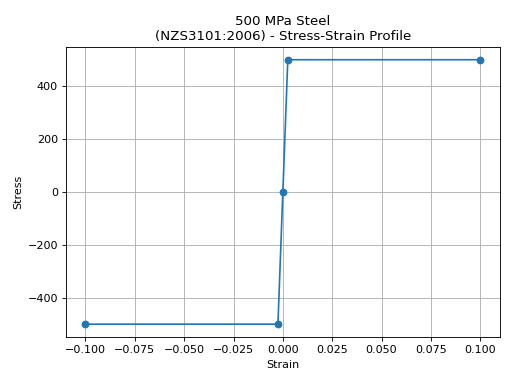
NZS3101.create_steel_material(steel_grade=None, yield_strength=None, fracture_strain=None, phi_os=None, colour='red')[source]

Returns a steel material object specific to the NZS3101:2006 code.

Material assumptions

Density: 7850 kg/m³
Elastic modulus: 200000 MPa
Stress-strain profile: Elastic-plastic, fracture strain \(\varepsilon_{su}\) from AS/NZS4671 Table 7.2(A) or NZSEE C5 assessment guidelines (for historic reinforcement grades)

Parameters: steel_grade (Optional[str], default: None) – Designation of the grade of reinforcement bar to be analysed, included predefined current and historic grades are as follows:-

Note

By using a valid steel grade designation the required input parameters are initiated with the required values for current reinforcement grades from the AS/NZS4671 standard or for historic grades from the NZSEE C5 assessment guidelines. Note user may overwrite any parameter of a predefined material by providing that parameter as input to NZS3101.create_steel_material().

Note if no predefined steel grade is provided, a steel grade name of ‘user_’ + yield strength is utilised.

NZS3101:2006 & NZSEE C5 asessment guidelines predefined steel materials

NZS3101:2006 characteristic yield strength based predefined materials

300e - Use for design to NZS3101:2006 provisions
- Characteristic yield strength \(f_y\) = 300 MPa
- Fracture strain \(\varepsilon_{su}\) = 15% or 0.15
- Overstrength factor \(\phi_{o,f_y}\) = 1.35
500e - Use for design to NZS3101:2006 provisions
- Characteristic yield strength \(f_y\) = 500 MPa
- Fracture strain \(\varepsilon_{su}\) = 10% or 0.10
- Overstrength factor \(\phi_{o,f_y}\) = 1.35

NZSEE C5 guidelines probable yield strength based predefined materials

pre_1945 - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 280 MPa
- Fracture strain \(\varepsilon_{su}\) = 10% or 0.10
- Overstrength factor \(\phi_{f_o}\) = 1.25
33 - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 280 MPa
- Fracture strain \(\varepsilon_{su}\) = 10% or 0.10
- Overstrength factor \(\phi_{f_o}\) = 1.25
40 - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 324 MPa
- Fracture strain \(\varepsilon_{su}\) = 15% or 0.15
- Overstrength factor \(\phi_{f_o}\) = 1.25
275 - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 324 MPa
- Fracture strain \(\varepsilon_{su}\) = 15% or 0.15
- Overstrength factor \(\phi_{f_o}\) = 1.25
hy60 - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 455 MPa
- Fracture strain \(\varepsilon_{su}\) = 12% or 0.12
- Overstrength factor \(\phi_{f_o}\) = 1.5
380 - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 455 MPa
- Fracture strain \(\varepsilon_{su}\) = 12% or 0.12
- Overstrength factor \(\phi_{f_o}\) = 1.5
430 - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 464 MPa
- Fracture strain \(\varepsilon_{su}\) = 12% or 0.12
- Overstrength factor \(\phi_{f_o}\) = 1.25
300 - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 324 MPa
- Fracture strain \(\varepsilon_{su}\) = 15% or 0.15
- Overstrength factor \(\phi_{f_o}\) = 1.25
500n - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 500 MPa
- Fracture strain \(\varepsilon_{su}\) = 5% or 0.05
- Overstrength factor \(\phi_{f_o}\) = 1.5
500 - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 540 MPa
- Fracture strain \(\varepsilon_{su}\) = 10% or 0.10
- Overstrength factor \(\phi_{f_o}\) = 1.25
cd_mesh - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 600 MPa
- Fracture strain \(\varepsilon_{su}\) = 1.5% or 0.015
- Overstrength factor \(\phi_{f_o}\) = 1.2
duc_mesh - Use for probable strength design to NZSEE C5 assessment guidelines
- Probable yield strength \(f_{yp}\) = 500 MPa
- Fracture strain \(\varepsilon_{su}\) = 3% or 0.03
- Overstrength factor \(\phi_{f_o}\) = 1.2

Parameters

yield_strength (Optional[float], default: None) –
Steel characteristic yield strength (MPa)
- Note for a predefined steel grade based on probable strength properties this is interpreted as the probable yield strength.
- Note for a user defined steel grade, this is always entered on the basis of a characteristic yield strength, even if undertaking a probable strength based analysis. The analysis will internally scale the characteristic yield stress by 1.08 as per NZSEE C5 assessment guidelines C5.4.3.
fracture_strain (Optional[float], default: None) – Lower bound tensile strain (\(\varepsilon_{su}\)), based on characteristic uniform elongation limit from AS/NZS4671 Table 7.2(A) or NZSEE C5 assessment guidelines Table C5.4.
phi_os (Optional[float], default: None) – Overstrength factor depending on reinforcement grade (\(\phi_{o,f_y}\) or \(\phi_o\)), refer to NZS3101:2006 CL 2.6.5.5, or for a probable strength assessment to the NZSEE C5 assessment guidelines refer to NZSEE C5 Table C5.4.
colour (str, default: 'red') – Colour of the steel for rendering, if user does not provide a value, characteristic strength based materials will be rendered as red, and probable strength based materials will be rendered as blue.

Raises

Exception – If a predefined steel grade is not provided and the required material properties have not been provided. For creating a user defined steel material, values for yield_strength, fracture_strain & phi_os are required to define a valid user defined material.

Returns

SteelBarNZ – Steel bar material object

from concreteproperties.design_codes.nzs3101 import NZS3101

design_code = NZS3101()
steel = design_code.create_steel_material(steel_grade="500E")

steel.stress_strain_profile.plot_stress_strain(
  title=f"{steel.name} - Stress-Strain Profile"
)

(Source code, png, hires.png, pdf)

6.2.2. Calculating Section Properties#

Analysis methods can be called from the NZS3101 object similar to ConcreteSection object. The following methods are identical to those found in the ConcreteSection object, i.e. do not apply any capacity reduction factors:

The following methods have been modified for NZS3101:2006, with codified capacity reduction factors applied.

NZS3101.ultimate_bending_capacity(pphr_class='NDPR', analysis_type='nom_chk', theta=0, n_design=0)[source]

Calculates the ultimate bending capacity with capacity factors to NZS3101:2006 or the NZSEE C5 assessment guidelines dependant on analysis type.

Parameters

analysis_type (str, default: 'nom_chk') – The type of cross section analysis to undertake on the defined concrete section, by default a normal nominal strength design check is undertaken, refer to NZS3101.capacity_reduction_factor() for further information on analysis types.
theta (float, default: 0) – Angle (in radians) the neutral axis makes with the horizontal axis (\(-\pi \leq \theta \leq \pi\))
n_design (float, default: 0) – Axial design force (\(N^*\))

Returns

Tuple[UltimateBendingResults, UltimateBendingResults, float] – Factored and unfactored ultimate bending results objects, and capacity reduction factor (factored_results, unfactored_results, phi)

NZS3101.moment_interaction_diagram(pphr_class='NDPR', analysis_type='nom_chk', theta=0, control_points=[('fy', 1.0), ('fy', 0.5), ('fy', 0.0), ('N', 0.0)], labels=None, n_points=24, n_spacing=None, max_comp_labels=None, progress_bar=True)[source]

Generates a moment interaction diagram with capacity factors and material strengths to NZS3101:2006 or the NZSEE C5 assessment guidelines dependant on analysis type.

Parameters

pphr_class (str, default: 'NDPR') –
Potential Plastic Hinge Region (PPHR) classification, NDPR/LDPR/DPR.
- NDPR = Nominally Ductile Plastic Region
- LDPR = Limited Ductile Plastic Region
- DPR = Ductile Plastic Region
analysis_type (str, default: 'nom_chk') – The type of cross section analysis to undertake on the defined concrete section, by default a normal nominal strength design check is undertaken, refer to NZS3101.capacity_reduction_factor() for further information on analysis types.
theta (float, default: 0) – Angle (in radians) the neutral axis makes with the horizontal axis (\(-\pi \leq \theta \leq \pi\))
control_points (List[Tuple[str, float]], default: [('fy', 1.0), ('fy', 0.5), ('fy', 0.0), ('N', 0.0)]) – List of additional control points to add to the moment interaction diagram. The default control points include the balanced point, the 50% reinforcement strain point, the 0% reinforcement strain point (fy=1, fy=0.5, fy=0), and the pure bending point (N=0). Control points may lie outside the limits of the moment interaction diagram as long as equilibrium can be found.
labels (Optional[List[str]], default: None) – List of labels to apply to the limits and control_points for plotting purposes. The first two values in labels apply labels to the limits, the remaining values apply labels to the control_points. If a single value is provided, this value will be applied to both limits and all control_points. The length of labels must equal 1 or 2 + len(control_points).
n_points (int, default: 24) – Number of points to compute including and between the limits of the moment interaction diagram. Generates equally spaced neutral axes between the limits.
n_spacing (Optional[int], default: None) – If provided, overrides n_points and generates the moment interaction diagram using n_spacing equally spaced axial loads. Note that using n_spacing negatively affects performance, as the neutral axis depth must first be located for each point on the moment interaction diagram.
max_comp_labels (Optional[List[str]], default: None) – Labels to apply to the max_comp intersection points, first value is at zero moment, second value is at the intersection with the interaction diagram.
progress_bar (bool, default: True) – If set to True, displays the progress bar

Returns

Tuple[MomentInteractionResults, MomentInteractionResults, List[float]] – Factored and unfactored moment interaction results objects, and list of capacity reduction factors (factored_results, unfactored_results, phis)

NZS3101.biaxial_bending_diagram(pphr_class='NDPR', analysis_type='nom_chk', n_design=0.0, n_points=48, progress_bar=True)[source]

Generates a biaxial bending with capacity factors to NZS3101:2006 or the NZSEE C5 assessment guidelines dependant on analysis type.

Parameters

pphr_class (str, default: 'NDPR') –
Potential Plastic Hinge Region (PPHR) classification, NDPR/LDPR/DPR.
- NDPR = Nominally Ductile Plastic Region
- LDPR = Limited Ductile Plastic Region
- DPR = Ductile Plastic Region
analysis_type (str, default: 'nom_chk') – The type of cross section analysis to undertake on the defined concrete section, by default a normal nominal strength design check is undertaken, refer to NZS3101.capacity_reduction_factor() for further information on analysis types.
n_design (float, default: 0.0) – Axial design force (\(N^*\))
n_points (int, default: 48) – Number of calculation points for neutral axis orientation
progress_bar (bool, default: True) – If set to True, displays the progress bar

Returns

Tuple[BiaxialBendingResults, List[float]] – Factored biaxial bending results object and list of capacity reduction factors (factored_results, phis).