cross-section analysis examples

Split 200 x 100 x 6 RHS

A box section provides torsional stiffness by providing a closed path for shear stresses to flow at a considerable distance from a rotational centre. Preventing this enclosed path dramatically reduces the torsional rigidity of the section. This is illustrated through the analysis and of a 200 x 100 x 6 RHS, and a comparison to that of the same section with a 1 mm wide cut in one of the sides. A torsion of 1 kN.m is applied to both sections.

The analysis can be carried out with the following python commands:

import sectionproperties.pre.sections as sections
from sectionproperties.analysis.cross_section import CrossSection

# create RHS geometry
rhs_geometry = sections.Rhs(d=100, b=200, t=6, r_out=15, n_r=16)

# create split RHS geometry
split_geometry = sections.Rhs(d=100, b=200, t=6, r_out=15, n_r=16)
# create points at split
p1 = split_geometry.add_point([99.5, 0])
p2 = split_geometry.add_point([99.5, 6])
p3 = split_geometry.add_point([101.5, 0])
p4 = split_geometry.add_point([101.5, 6])
# create facets at split
split_geometry.add_facet([p1, p2])
split_geometry.add_facet([p3, p4])
split_geometry.add_hole([100, 3])  # add hole
split_geometry.clean_geometry()  # clean the geometry

# create mesh and CrossSection objects
rhs_mesh = rhs_geometry.create_mesh(mesh_sizes=[2.5])
split_mesh = split_geometry.create_mesh(mesh_sizes=[2.5])
rhs_section = CrossSection(rhs_geometry, rhs_mesh)
split_section = CrossSection(split_geometry, split_mesh)

# plot the meshes
rhs_section.plot_mesh(pause=False)
split_section.plot_mesh()

# perform a geometric, warping analysis and stress analyses
print("CLOSED RHS:")
rhs_section.calculate_geometric_properties(time_info=True)
rhs_section.calculate_warping_properties(time_info=True)
rhs_stress = rhs_section.calculate_stress(Mzz=1e6, time_info=True)
print("\nSPLIT RHS:")
split_section.calculate_geometric_properties(time_info=True)
split_section.calculate_warping_properties(time_info=True)
split_stress = split_section.calculate_stress(Mzz=1e6, time_info=True)

# print torsional constants
print("Torsion Constants:")
print("CLOSED RHS: {0:.5e}".format(rhs_section.get_j()))
print("SPLIT RHS: {0:.5e}".format(split_section.get_j()))

# plot the stress
rhs_stress.plot_stress_mzz_zxy(pause=False)
rhs_stress.plot_vector_mzz_zxy(pause=False)
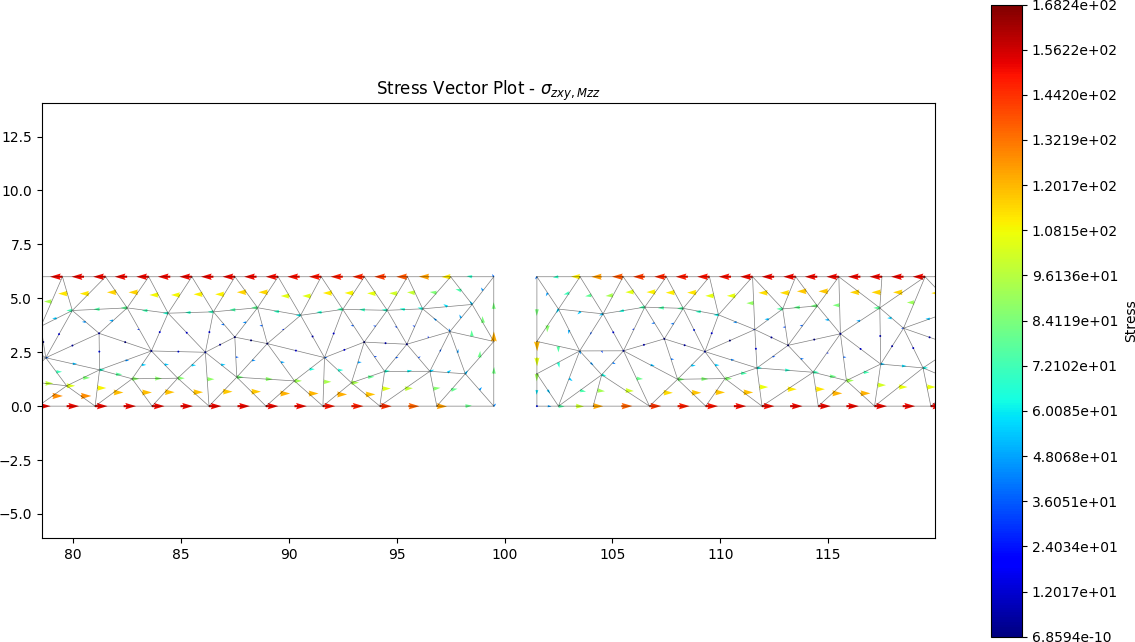
split_stress.plot_stress_mzz_zxy(pause=False)
split_stress.plot_vector_mzz_zxy()

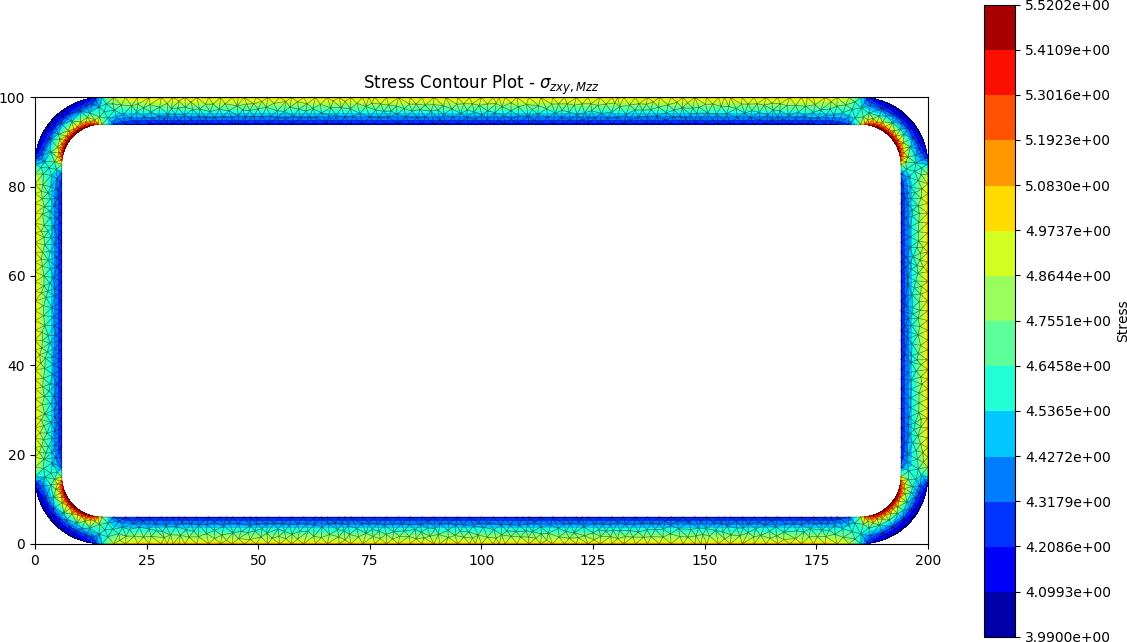
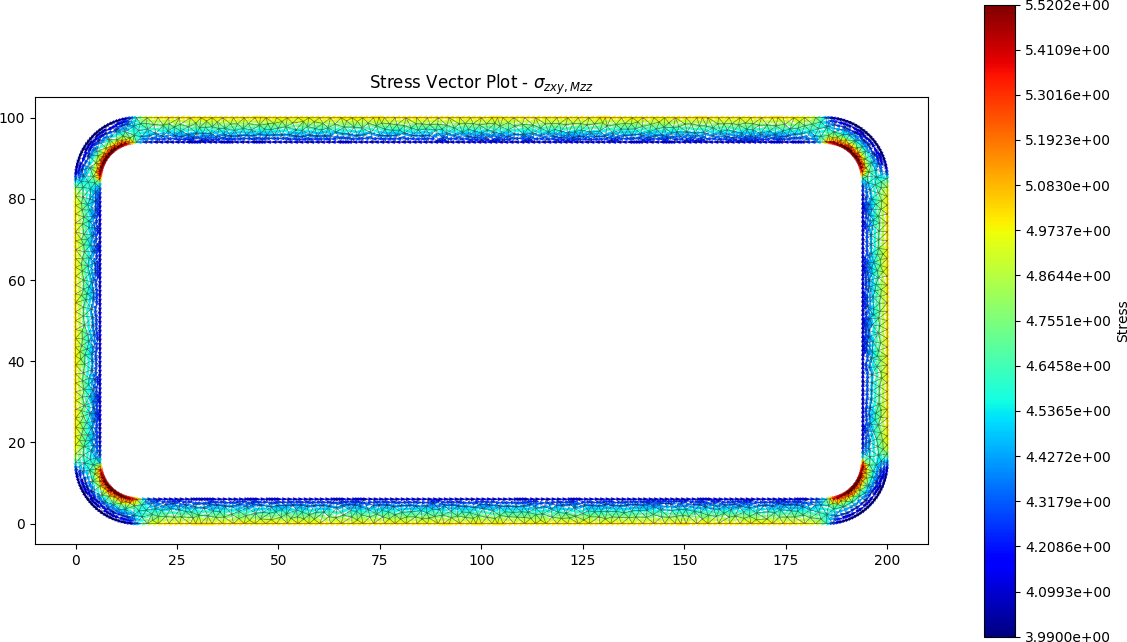
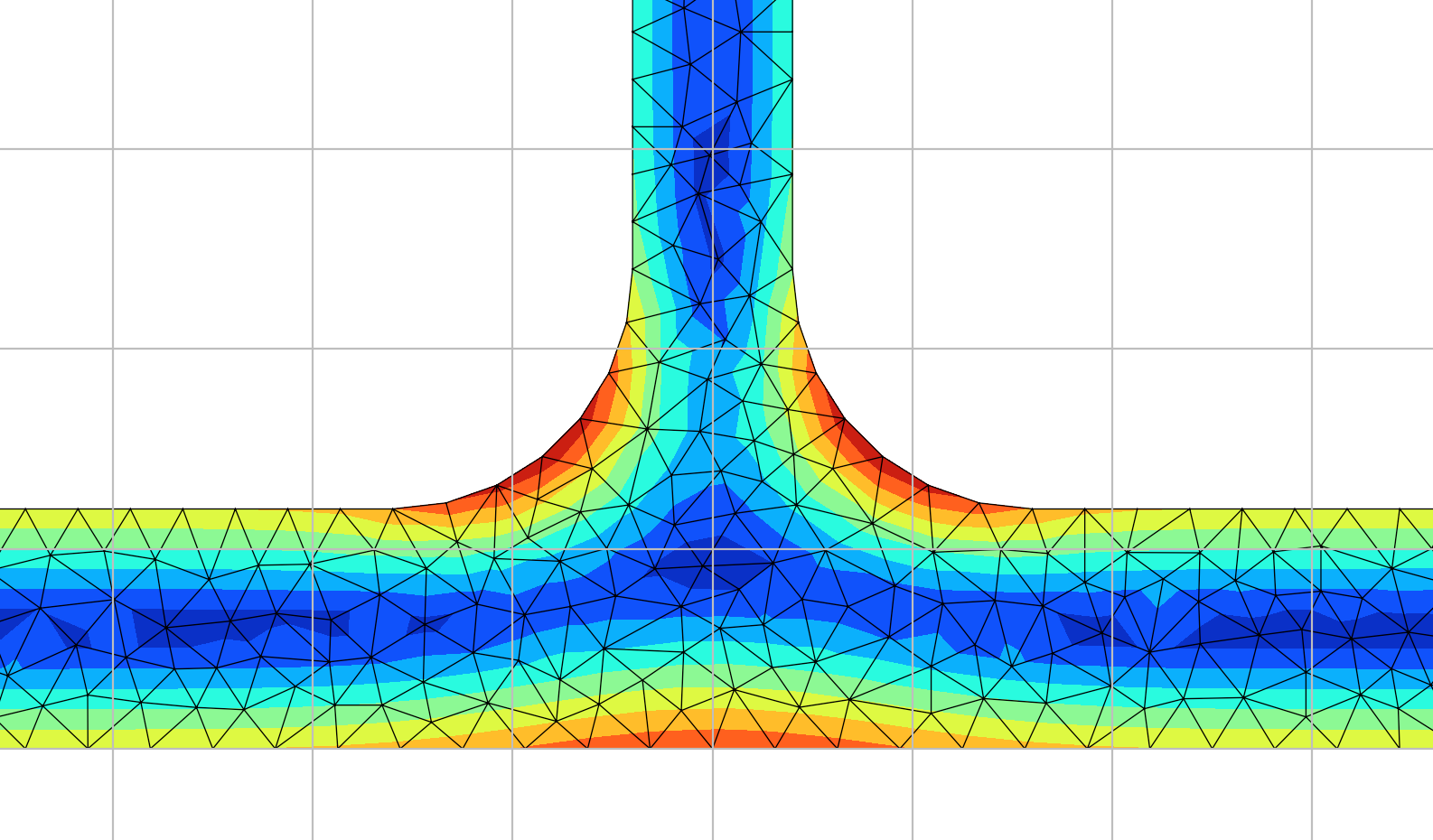
Closed RHS results

The torsion constant was calculated by the python package to be J = 14.236 x 10⁶ mm⁴.

Mesh discretisation for the closed 200 x 100 x 6 RHS.

Shear stress due to torsion for the closed 200 x 100 x 6 RHS.

Shear stress vectors due to torsion for the closed 200 x 100 x 6 RHS at the top right of the section.

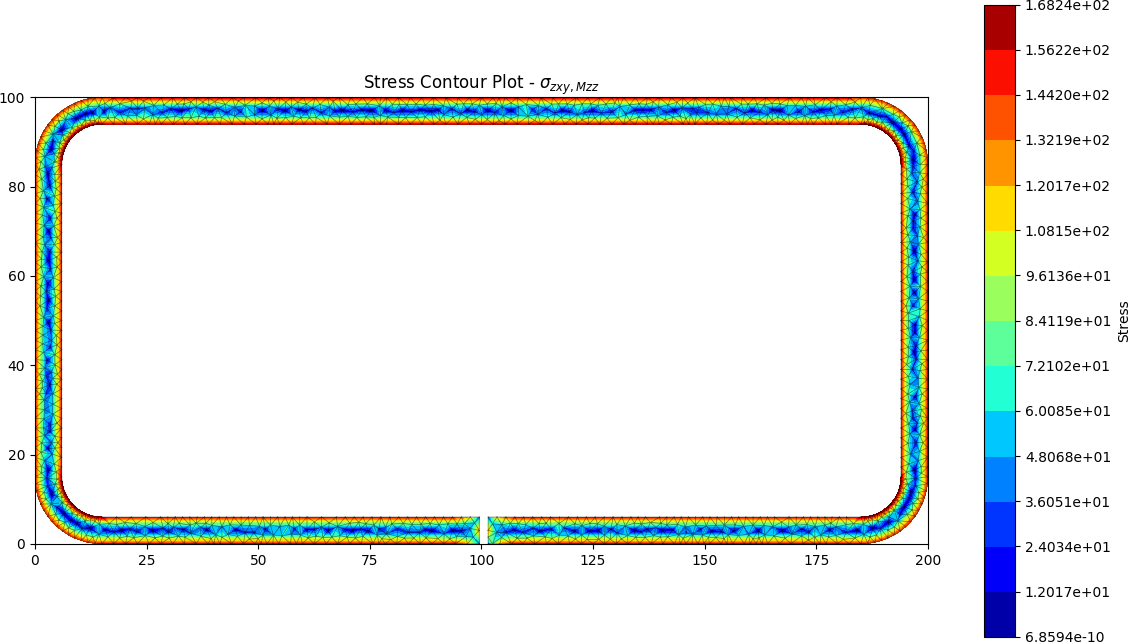
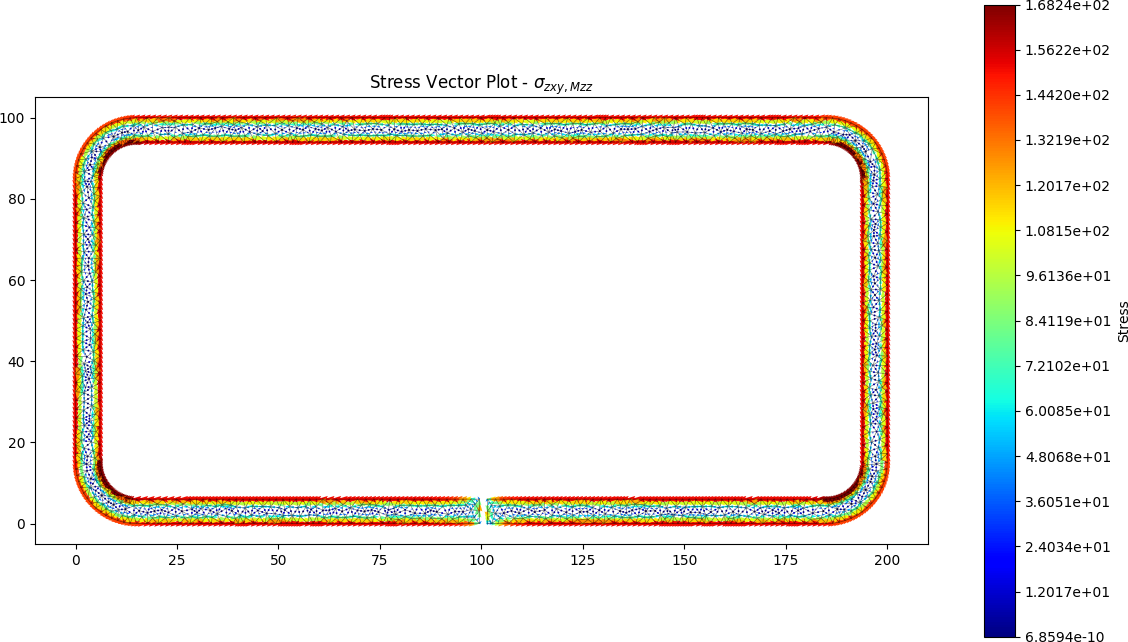
Split RHS results

The torsion constant was calculated by the python program to be J = 39.648 x 10³ mm⁴, approximately 360 times less stiff than the closed section.

Mesh discretisation for the split 200 x 100 x 6 RHS.

Shear stress due to torsion for the split 200 x 100 x 6 RHS, approximately 30 times higher than the closed section.

Shear stress vectors due to torsion for the split 200 x 100 x 6 RHS at the top right of the section. The shear stress now has to flow within the thickness of the wall, rather than around the entire section.

Shear stress vectors due to torsion for the split 200 x 100 x 6 RHS adjacent to the split.

250 PFC

The analysis of a 250 PFC (250 mm deep parallel flange channel) can be carried out with the following python commands:

import sectionproperties.pre.sections as sections
from sectionproperties.analysis.cross_section import CrossSection

# create PFC geometry
geometry = sections.PfcSection(d=250, b=90, t_f=15, t_w=8, r=12, n_r=16)

# create a mesh
mesh = geometry.create_mesh(mesh_sizes=[4])

# create a CrossSection object
section = CrossSection(geometry, mesh)

# perform a geometric, warping and plastic analysis
section.calculate_geometric_properties()
section.calculate_warping_properties()
section.calculate_plastic_properties()

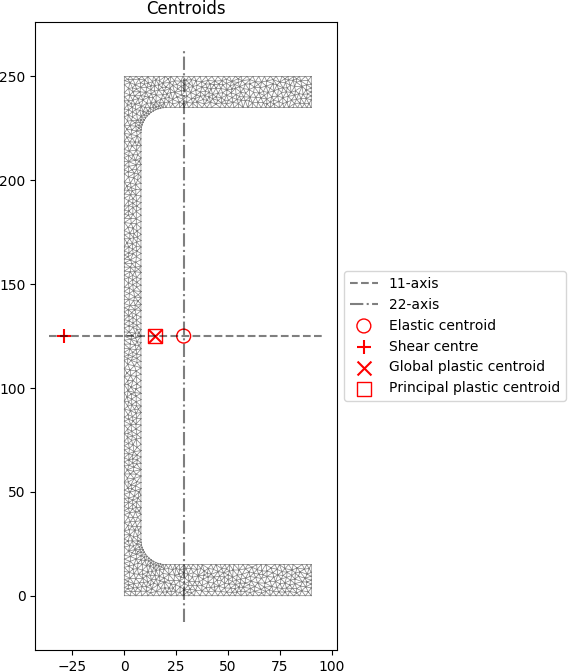
# plot the centroids
section.plot_centroids()

# get the torsion constant, warping constant and shear centre
print("Torsion Constant: {0:.5e}".format(section.get_j()))
print("Warping Constant: {0:.5e}".format(section.get_gamma()))
(cx, _) = section.get_c()
(x_s, _) = section.get_sc()
print("Shear Centre: {0:.5e}".format(x_s - cx))

Mesh discretisation for the 250 PFC with principal axes and centroids.

This produces the following output for the warping dependent properties:

$$J = 237.85 \times 10^3 \textrm{mm}^4 \\ I_w = 35.556 \times 10^9 \textrm{mm}^6 \\ x_s = -57.758 \textrm{mm}$$

These results, which use a mesh size of 4 mm², can be compared to the tabulated values in the OneSteel catalogue, and simple hand calculations. The OneSteel catalogue gives the following properties:

$$J = 248 \times 10^3 \textrm{mm}^4 \\ I_w = 35.9 \times 10^9 \textrm{mm}^6 \\ x_s = -58.5 \textrm{mm}$$

A mesh refinement study using the python cross-section package shows that the OneSteel value for the torsion constant is slightly (4%) overestimated, whereas the warping constant and shear centre show closer convergence. The numerical results obtained from the python package can be compared to simple hand calculations:

• Torsion Constant [1]

$$J \approx \sum \left(\frac{b t^3}{3}\right) = 240.0 \times 10^3 \textrm{mm}^4$$

• Warping Constant [1]

$$I_w = \frac{ {b_f}^3 t_f {b_w}^2 }{48} \left(8 - \frac{3 b_f t_f {b_w}^2 }{I_x}\right) = 40.29 \times 10^9 \textrm{mm}^6$$

• Shear Centre [2] (from centre of web to shear centre):

$$x_s = -x_c + \frac{t_w}{2} -\frac{3 t_f (b_f - 0.5t_w)^2 }{6 (b_f - 0.5t_w) t_f + (d - t_f) t_w} = 59.20 \textrm{mm}$$

The above hand calculations align well with the results from the python package and the OneSteel catalogue.

Built-up 200UB25 + 150 x 100 x 9 RHS

A steel section is fabricated by placing a 150 x 100 x 9 RHS on its side on top of a 200UB25. The section is subjected to a major axis bending moment of 50 kN.m, a torsion moment of 10 kN.m and a y-direction shear force of -25 kN.

The analysis can be carried out by using the section builder function with the following python commands:

import sectionproperties.pre.sections as sections
from sectionproperties.analysis.cross_section import CrossSection

# create geometry
ub_geometry = sections.ISection(d=203, b=133, t_f=7.8, t_w=5.8, r=8.9, n_r=8, shift=[-66.5, 0])
rhs_geometry = sections.Rhs(d=100, b=150, t=9, r_out=22.5, n_r=8, shift=[-75, 203])
geometry = sections.MergedSection([ub_geometry, rhs_geometry])  # merge the sections
geometry.clean_geometry()  # clean the geometry

# create a mesh
mesh = geometry.create_mesh(mesh_sizes=[5, 5])

# create a CrossSection object
section = CrossSection(geometry, mesh)
section.plot_mesh()

# perform a geometric, warping, plastic and stress analysis
section.calculate_geometric_properties()
section.calculate_warping_properties()
section.calculate_plastic_properties()
stress = section.calculate_stress(Mxx=50e6, Mzz=10e6, Vy=-25e3)

# plot the centroids
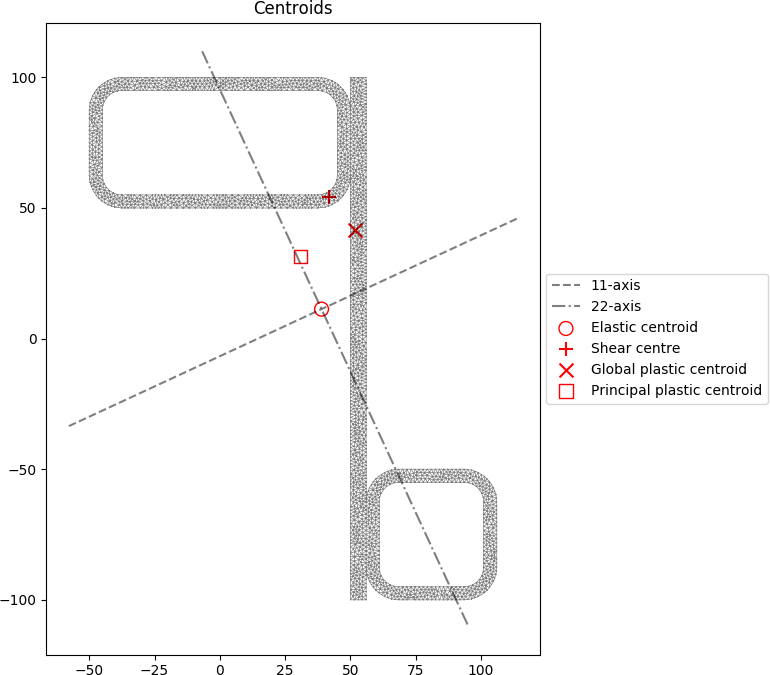
section.plot_centroids()

# plot the stress
stress.plot_stress_m_zz(pause=False)
stress.plot_stress_mzz_zxy(pause=False)
stress.plot_stress_v_zxy(pause=False)
stress.plot_stress_vm()

The centroids and stress contours are shown below:

Mesh discretisation for the built-up section with principal axes and centroids.

Bending stress.

Shear stress due to torsion.

Shear stress due to transverse shear force.

von Mises stress.

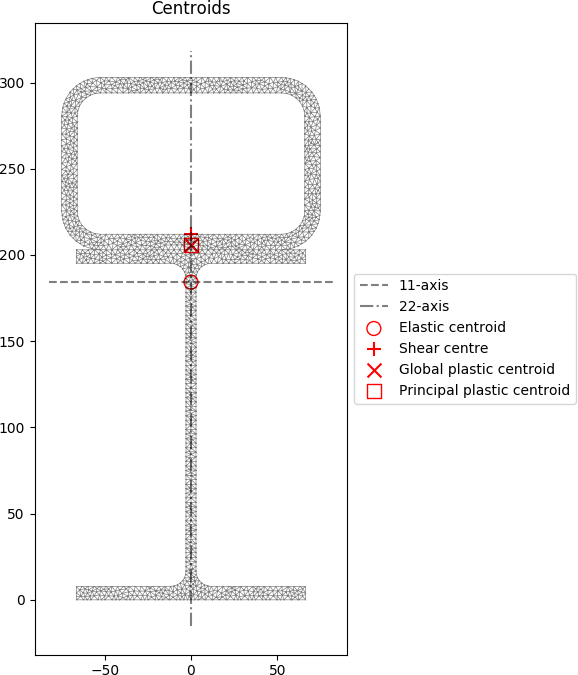
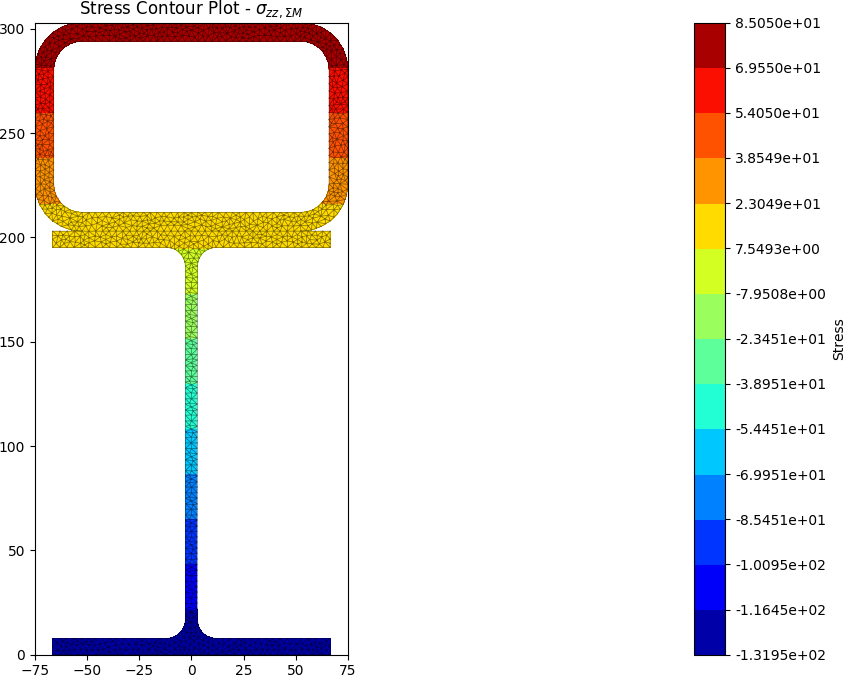
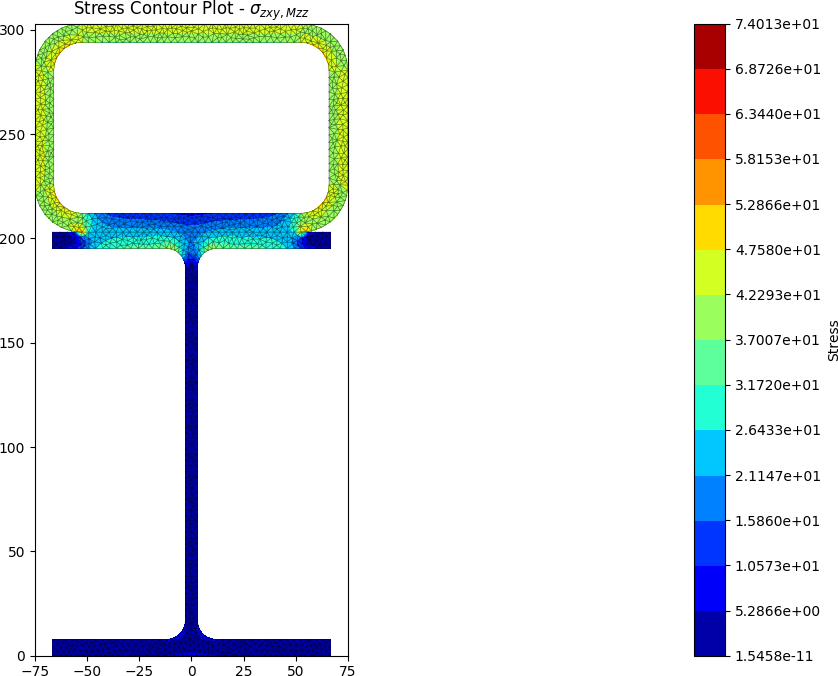
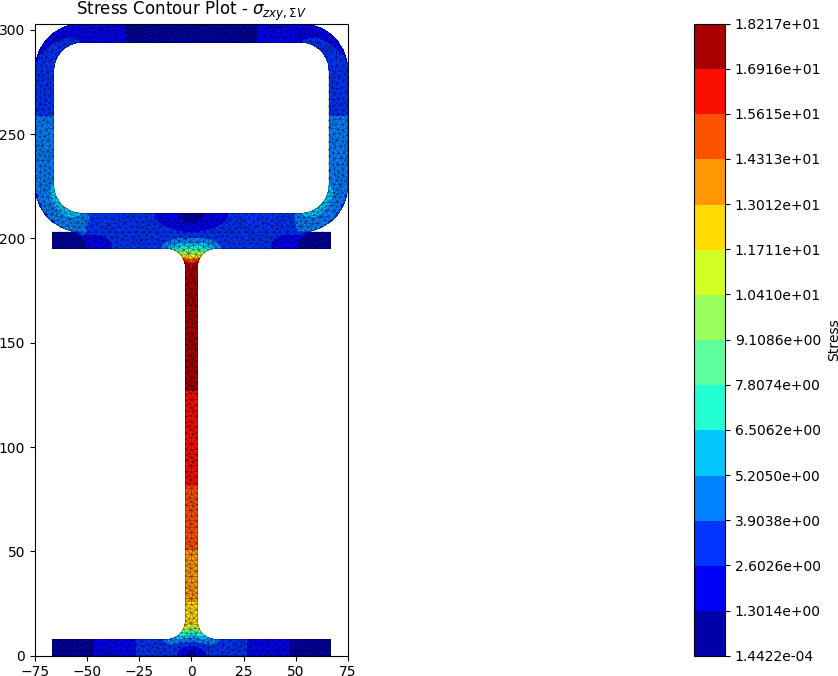
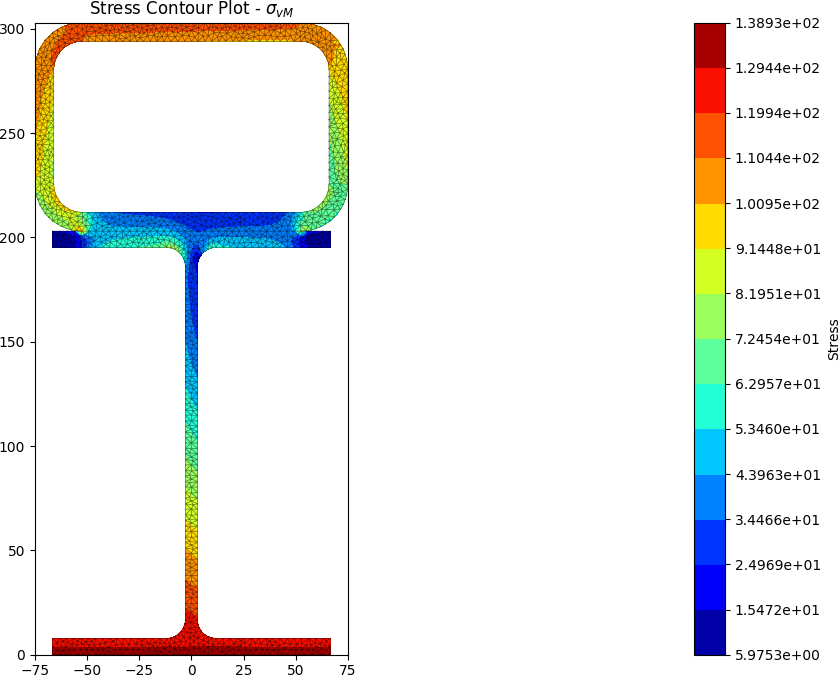
Built-up 50 x 5 SHS + 100 x 50 x 5 RHS + 200 x 6 Flat

A zed shaped steel section is fabriacted by welding a 50 x 5 SHS and a 100 x 50 x 5 RHS to a 200 x 6 flat section. The section is subjected to a major axis bending moment of 10 kN.m, a torsion moment of 5 kN.m and a y-direction shear force of -15 kN.

The analysis can be carried out by using the section builder function with the following python commands:

import sectionproperties.pre.sections as sections
from sectionproperties.analysis.cross_section import CrossSection

# create geometry
flat_geometry = sections.RectangularSection(d=200, b=6, shift=[50, -100])
shs_geometry = sections.Rhs(d=50, b=50, t=5, r_out=12.5, n_r=8, shift=[56, -100])
rhs_geometry = sections.Rhs(d=50, b=100, t=5, r_out=12.5, n_r=8, shift=[-50, 50])
# merge the sections
geometry = sections.MergedSection([flat_geometry, shs_geometry, rhs_geometry])
geometry.clean_geometry()  # clean the geometry

# create a mesh
mesh = geometry.create_mesh(mesh_sizes=[1.5, 1.5, 1.5])

# create a CrossSection object
section = CrossSection(geometry, mesh)
section.plot_mesh()

# perform a geometric, warping, plastic and stress analysis
section.calculate_geometric_properties()
section.calculate_warping_properties()
section.calculate_plastic_properties()
stress = section.calculate_stress(Mxx=10e6, Mzz=5e6, Vy=-15e3)

# plot the centroids
section.plot_centroids()

# plot the stress
stress.plot_stress_m_zz(pause=False)
stress.plot_stress_mzz_zxy(pause=False)
stress.plot_stress_v_zxy(pause=False)
stress.plot_stress_vm()

The centroids and stress contours are shown below:

Mesh discretisation for the built-up section with principal axes and centroids.

Bending stress.

Shear stress due to torsion.

Shear stress due to transverse shear force.

von Mises stress.

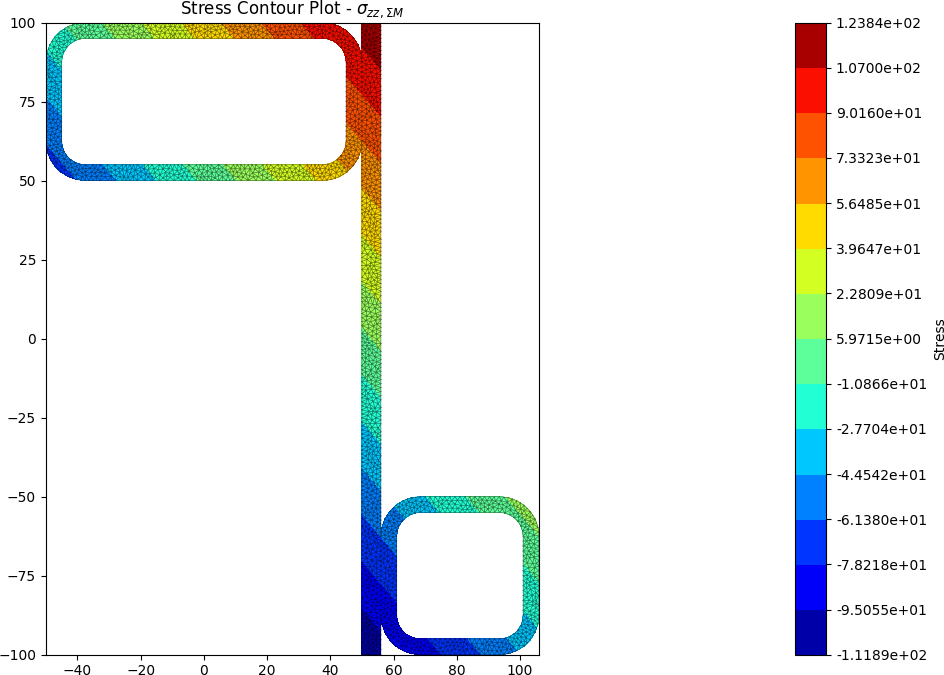
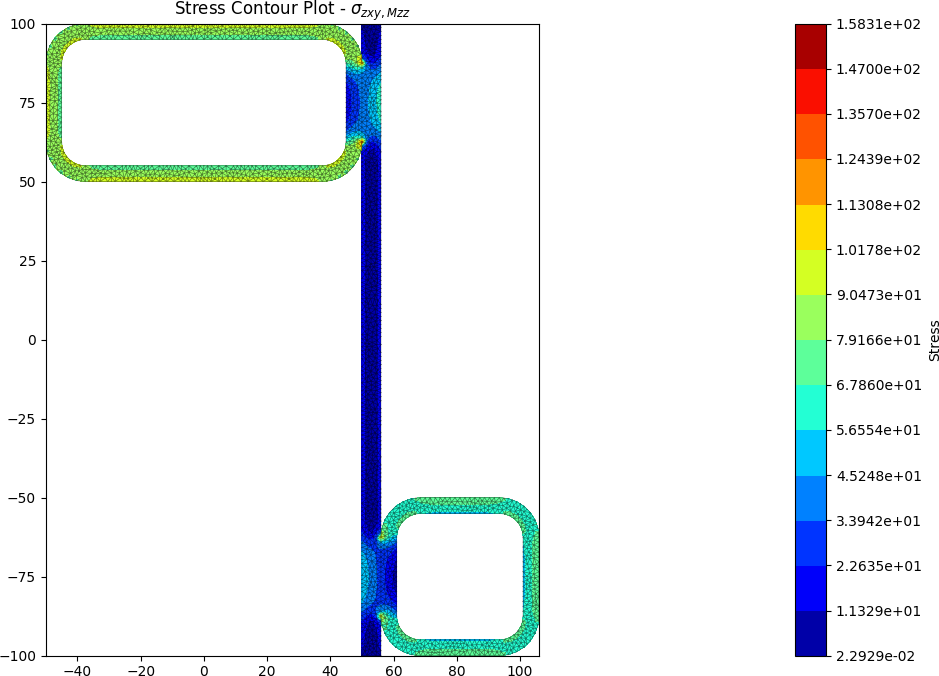
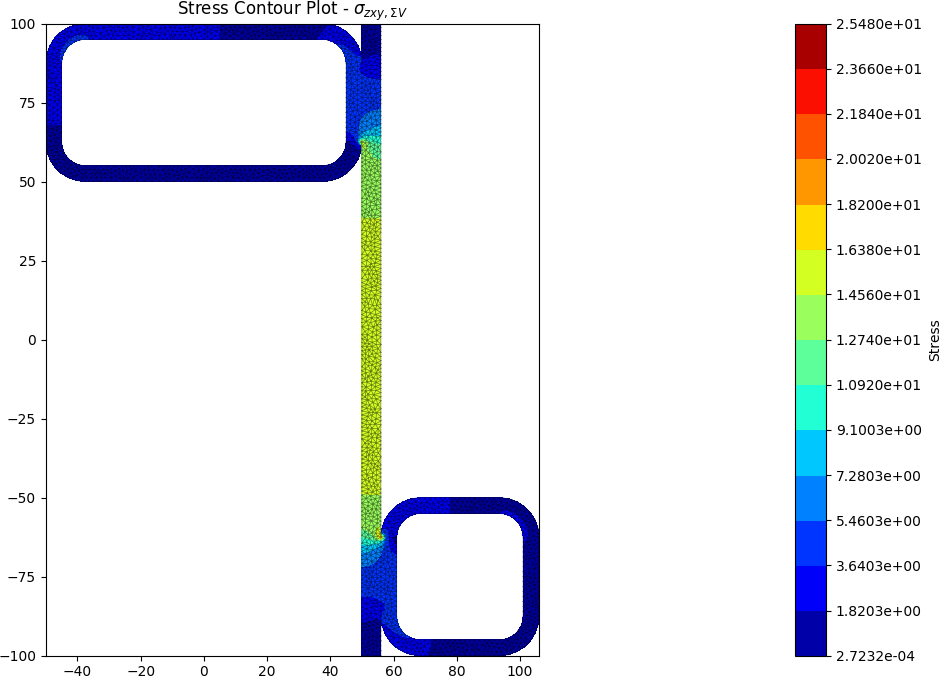
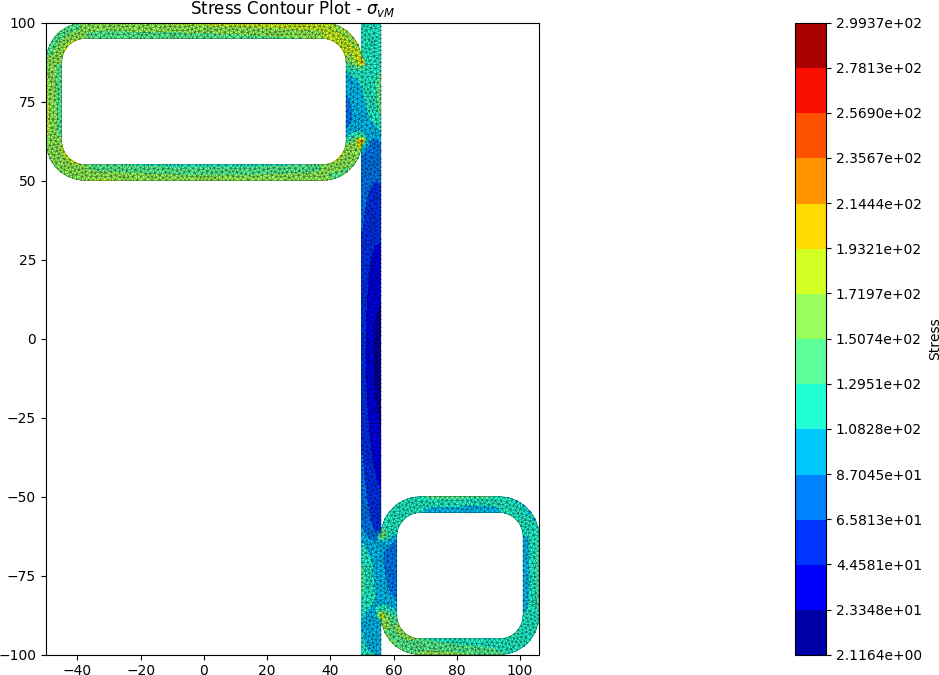
References

1. AS 4100-1998: Steel Structures
2. W.D. Pilkey, Analysis and Design of Elastic Beams: Computational Methods, John Wiley & Sons, Inc., New York, 2002.