This post presents an overview of my Masters thesis in Computational Mechanics which I completed in June 2018. If you are interested in reading my thesis, you can find it on the TU Delft repository or you can download the entire report here.
Overview
Epoxy resins are increasingly used in critical structural components with widespread applications in the transportation, construction and energy industries. One such application is in wind turbine blades, where the structural components are predominantly constructed from glass/epoxy composites, or fibreglass. In offshore installations, these blades are subject to a wide range of environmental conditions, most notably large variations in humidity and temperature. Both moisture and increased temperatures have been observed to have a significant impact on the stiffness and strength of epoxy resins. These environmental effects, coupled with complex time dependent mechanical behaviour, means that the accurate prediction of the structural performance of epoxy resins has not yet been fully described.
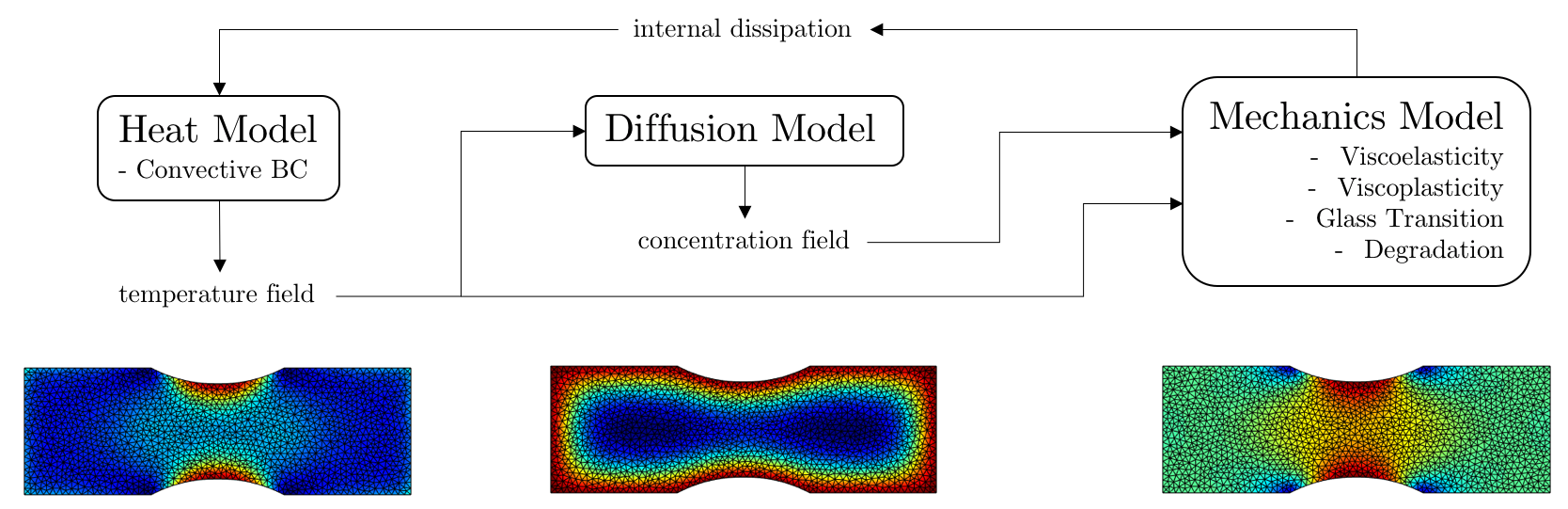
In my thesis I presented a multiphysics framework for the simulation of hygrothermal ageing in epoxy resins. The constitutive model consisted of a non-linear viscoelastic and viscoplastic mechanical model, physically coupled with a Fourier heat conduction model and a Fickian diffusion model. Material degradation based on a glass transition surface was implemented to describe the multi-state behaviour of epoxy resins. A number of numerical benchmark tests and case studies were performed using a finite element implementation of the numerical framework and it was shown that the multiphysics framework can capture the characteristic mechanical and hygrothermal ageing behaviour exhibited by epoxy resins. In this post I will highlight the key features of each component of the multiphysics model and present some of the interesting results.
Multiphysics Numerical Framework
Heat Conduction and Moisture Diffusion
Both heat conduction and moisture diffusion follow similar formulations based on the governing laws of Fourier heat conduction and Fickian diffusion. Fourier heat conduction states that heat flux is proportional to the negative gradient of the temperature:
Fickian diffusion is analogous to Fourier heat conduction in that the moisture flux is proportional to the negative gradient of the moisture concentration:
When combined with the conservation laws, the strong formulation of these transport problems can be obtained. Inline with finite element theory, the weak form can be obtained by considering relevant the boundary conditions. The transient formulation of the transport processes produces the assembly of element level matrices and vectors. In this blog post, the finite element formulation of the heat conduction model is presented. For a full derivation of both formulations, the reader is referred to the full report referred to at the top of this page. The finite element formulation of the heat conduction model is:
where is the element assembly operator, is the element temperature, and the element level matrices and vectors are given by:
Mechanical Model
The mechanical model follows from the classical continuum small strain formulation, resulting in the following finite element formulation:
where is the element displacement vector, and the element level matrices and vectors are given by:
Of main interest in this thesis is the determination of the material constitutive matrix for epoxy resins and the resulting stress vector . The ingredients that contribute to this constitutive attempt to characterise the mechanical behaviour of epoxy resins and in this thesis consist of the following:
- Non-linear viscoelasticity
- Viscoplasticity
- Glass transition surface
- Material degradation
Non-linear Viscoelasticity
The non-linear viscoelasticity model was implemented to capture time dependent elastic behaviour as well as the non-linear recoverable elastic behaviour exhibited by epoxy resins. In this model the elastic stress is decomposed into a long term elastic component and a viscoelastic component:
The expression for the viscoelastic stress can be further decomposed into a volumetric component and a deviatoric component :
In the above equations the function introduces non-linearity into the viscoelastic model. The finite element implementation of the above formulation is further elaborated in the full report. Following from the finite element formulation of the stress vector, the tangent stiffness can also be derived.
Viscoplasticity
A viscoplasticity model was implemented to capture the time dependent plastic behaviour of epoxy resins. The formulation used in my thesis followed from the model used by Rocha et. al. [24]. In order to combine a non-linear viscoelasticity model with a viscoplasticity model, a coupled return mapping scheme was derived and implemented in the context of the Newton-Raphson method to ensure robust and efficient convergence. The essence behind this implementation is that the degree of non-linear viscoelasticity and the degree of plasticity, defined by the plastic multiplier , are determined using the coupled Jacobians of the iterative functions:
Glass Transition Surface
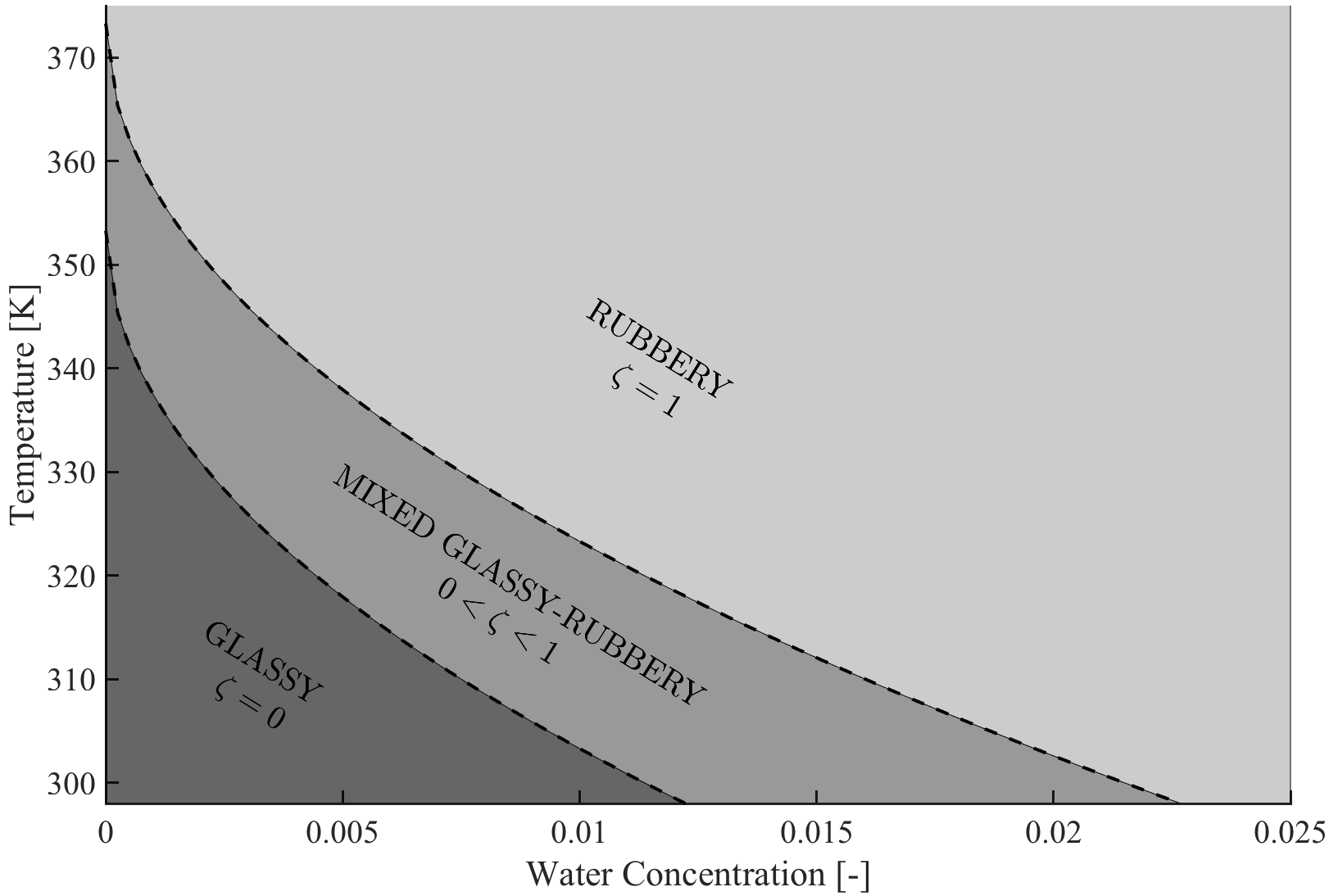
The idea of the glass transition surface is to relate both the temperature and moisture content of the epoxy resin to its material state. Conceptually an epoxy resin, or in general a polymer, can exist in three different material states: glassy, rubbery and mixed glassy-rubbery. Glassy behaviour occurs at lower temperatures and moisture contents and is characterised by stiffer and stronger material behaviour. On the other hand, rubbery behaviour occurs at higher temperatures and moisture contents and is characterised by softer and weaker material behaviour. In this thesis the material state is related to a scalar parameter which characterises the degree of glass transition:
- Glassy behaviour:
- Mixed glassy-rubbery behaviour:
- Rubbery behaviour:
The simplicity of the glass transition model is that the state of the material can be described by the temperature and moisture content of the epoxy resin and can easily be calibrated to a specific epoxy resin system.
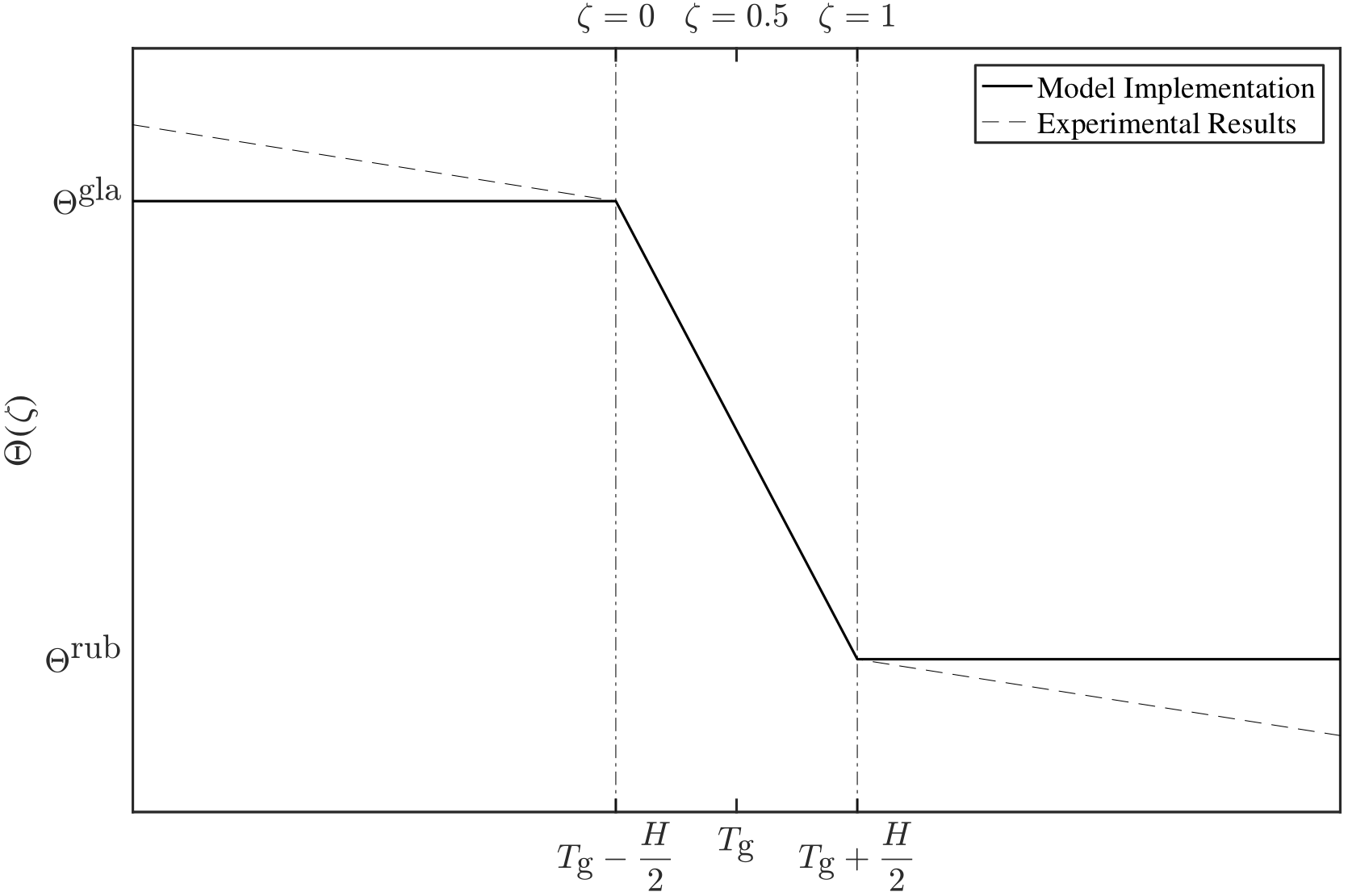
Material Degradation
The purpose of the degradation model is to relate the current state of the epoxy resin to its current material properties. The relevant material properties of the epoxy resin are assumed to be constant in the glassy and rubbery states, and are linearly interpolated based on the degree of glass transition in the mixed state. The state dependent material properties are generalised as follows:
While this method simplifies the material behaviour by imposing a constant property when the epoxy resin is in a glassy or rubbery state and a linearly interpolated property for the mixed state, this assumption has been found to give reasonably accurate results.
Multiphysics Fatigue Analysis
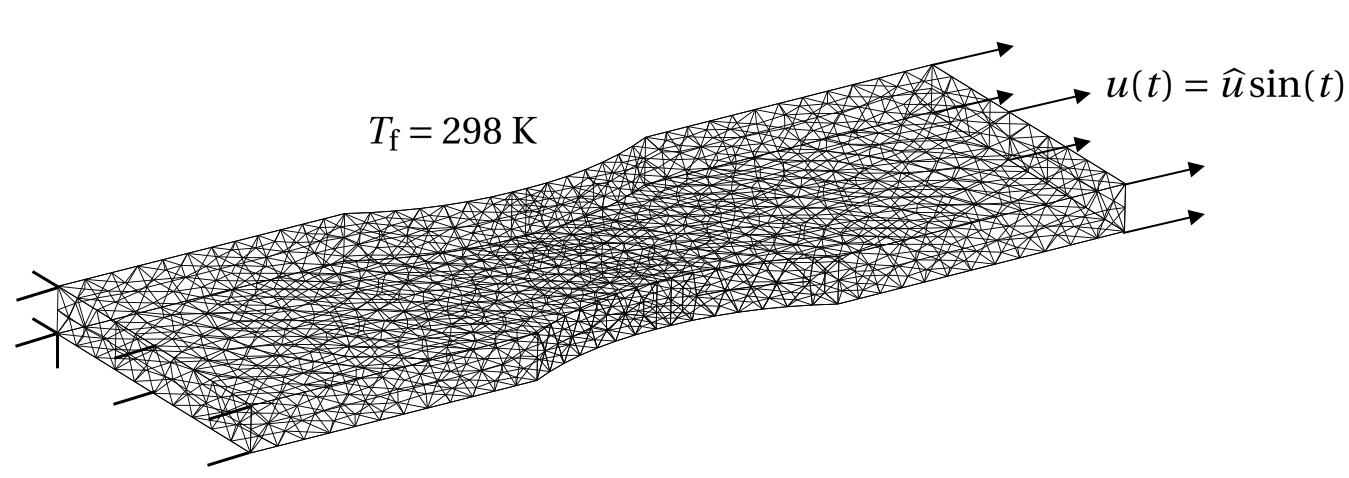
Using a finite element implementation of the aforementioned multiphysics model, a fatigue test was numerically performed on an epoxy resin sample. A dogbone sample, initially at room temperature, was surrounded by air at room temperature. A cyclic load was applied to the end of the specimen at a high strain rate in order to significantly increase the temperature of the epoxy resin. The multiphysics model formulated in my thesis is able to capture the competing processes of internal heat generation from viscous mechanical deformation and dissipative cooling by the surrounding fluid.
The simulation is summarised in the animation below, in which the temperature of the epoxy resin, the longitudinal stress distribution and the material state are plotted within the specimen. Also presented is the load displacement diagram and a plot of the temperature and degree of glass transition.
The multiphysics framework is able to capture the glass transition that occurs due to the heat generated by mechanical deformation. This glass transition occurs first at the edges of the specimen where the stress concentration is the highest. A corresponding redistribution of stress towards the centre of the element accompanies this material state transition as the load moves away from the softening material at the edges. Eventually the entire central section of specimen transitions to a rubbery state and a uniform stress distribution is obtained. This characteristic cyclic softening is further highlighted in the load displacement plot in which a softening of the material response, entirely induced by cyclic loading, occurs after approximately 3000 cycles.
Conclusions
A numerical multiphysics model using the finite element framework was formulated for epoxy resins in order to capture complex time dependent mechanical and hygrothermal behaviour. The fatigue test illustrated that the model was able to capture many aspects of the multiphysical behaviour of epoxy resins, such as time dependent mechanical effects, cyclic relaxation and softening, and deformation induced glass transition.
Not mentioned in this blog, but covered in the full report, are further topics related to numerically describing the behaviour of epoxy resins:
- Assessment of the non-linear viscoelasticity model
- Experiments (DMA and creep tests) conducted on epoxy resin samples
- Mesh sensitivity studies on a continuum damage model for epoxy resins
- Recommendations for future work related to the ideas presented in my thesis




Leave a comment